geometria-solida/index.md

layout	css	title
main	main	Geometria Solida

Lo spazio e la geometria solida

Postulati dello spazio

Postulato n. 1

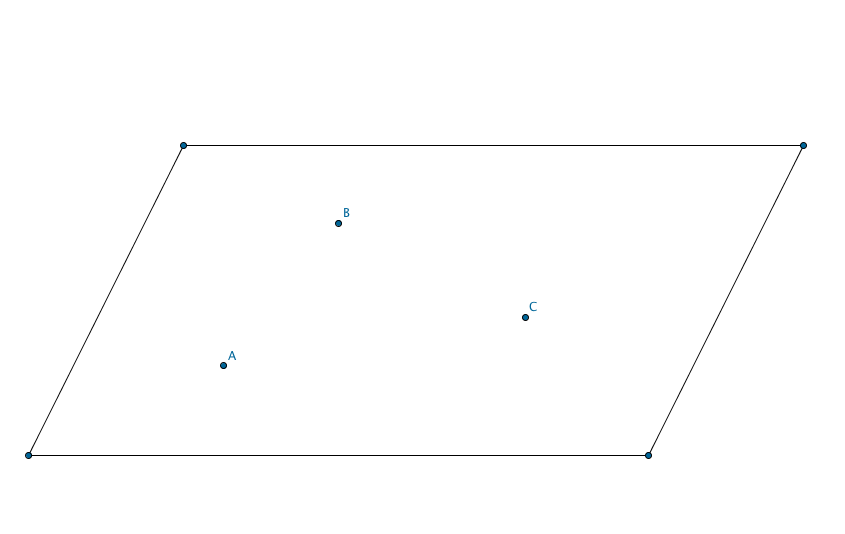
Per tre punti non allineati passa uno e un solo piano.

Postulato n. 2

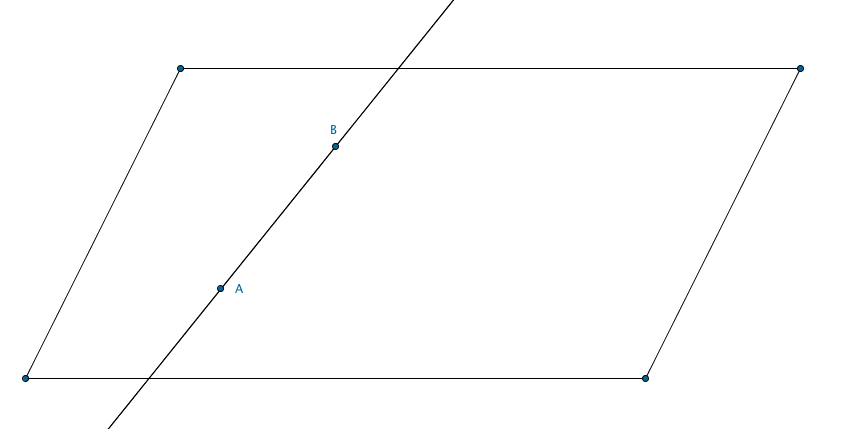
Fissati due punti in un piano, la retta passante per i due punti giace interamente sul piano.

Postulato di partizione dello spazio

Un qualunque piano divide l’insieme dei punti dello spazio che non gli appartengono in due regioni dette semispazi con le seguenti proprietà:

• due punti qualsiasi della stessa regione sono gli estremi di un segmento che non interseca il piano;
• due punti qualsiasi di regioni diverse sono gli estremi di un segmento che interseca il piano. Il piano si dice origine dei semispazi.

Rette nello spazio

Posizione di due rette nello spazio

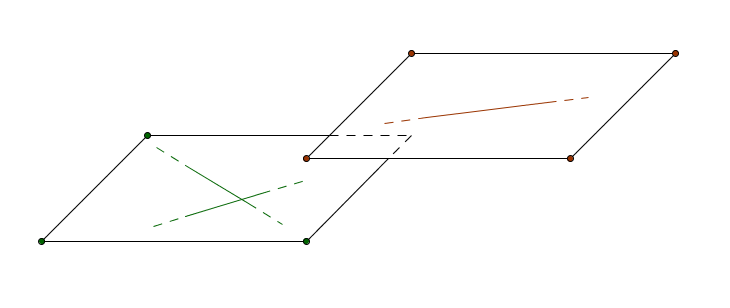
Due rette che giacciono sullo stesso piano, si dicono complanari, altrimenti si dicono sghembe.

Posizione di due piani nello spazio

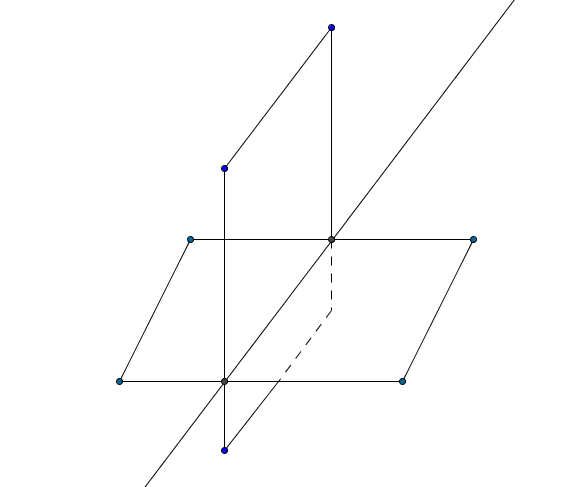
Due piani distinti, che si intersecano in un punto, hanno in comune una retta che passa per quel punto.

Rette perpendicolari a un piano

• Se per un punto P di una retta \mathscr{s} si mandano due rette \mathscr{a} e \mathscr{b} perpendicolari a \mathscr{s}, allora \mathscr{s} è perpendicolare a ogni altra retta \mathscr{r} passante per P e giacente sul piano delle rette \mathscr{a} e \mathscr{b}.

• Le perpendicolari a una retta \mathscr{s} condotte per un suo punto P giacciono tutte nello stesso piano.

• Due rette perpendicolari a uno stesso piano sono parallele fra loro.

• Dati un piano \alpha e un punto P, esiste ed è unica la retta r passante per il punto e perpendicolare al piano.

• Se due piani sono perpendicolari a una stessa retta in punti distinti, allora sono paralleli.

• Le intersezioni tra un piano e due piani paralleli sono rette parallele.

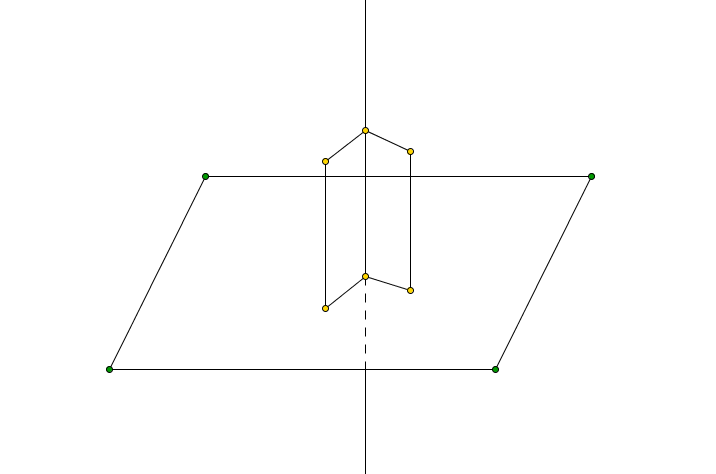
Teorema delle tre perpendicolari

Se dal piede di una perpendicolare a un piano si manda la perpendicolare a una qualunque retta del piano, quest'ultima risulta perpendicolare al piano delle prime due.

Dimostrazione

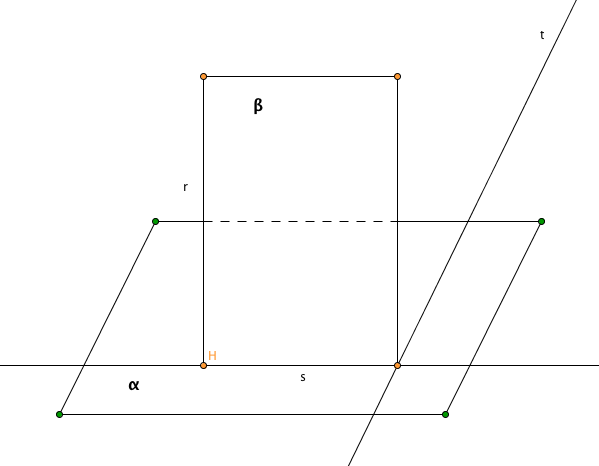
Siano \mathscr{r} la retta perpendicolare al piano \alpha per H, t una qualunque retta giacente su \alpha non passante per H e \mathscr{s} la perpendicolare a \mathscr{t} passante per H.
Siano S l'intersezione tra \mathscr{t} e \mathscr{s}, P e Q due punti su t tali che PS \cong PQ e T un punto qualunque su \mathscr{r}.

Considero \triangle HSQ e \triangle HSP. Essi hanno:

• HS in comune
• PS \cong PQ per costruzione
• HS \perp s

\triangle HSQ \cong \triangle HSP per il 1° criterio di congruenza. In particolare hanno HQ \cong HP

Considero \triangle THQ e \triangle THP. Essi hanno:

• TH in comune
• PS \cong PQ per dimostrazione precedente
• T\widehat{H}Q \cong T\widehat{H}P perché retti

\triangle THQ \cong \triangle THP per il 1° criterio di congruenza. In particolare hanno TQ \cong TP

Considero \triangle TSQ e \triangle TSP. Essi hanno:

• TS in comune
• TQ \cong TP per dimostrazione precedente
• QS \cong SP perché retti

\triangle TSQ \cong \triangle TSP per il 3° criterio di congruenza. In particolare hanno T\widehat{S}Q \cong T\widehat{S}P.

T\widehat{S}Q \cong T\widehat{S}P \cong \widehat{R} \Rightarrow TS \perp s \Rightarrow s \perp \beta

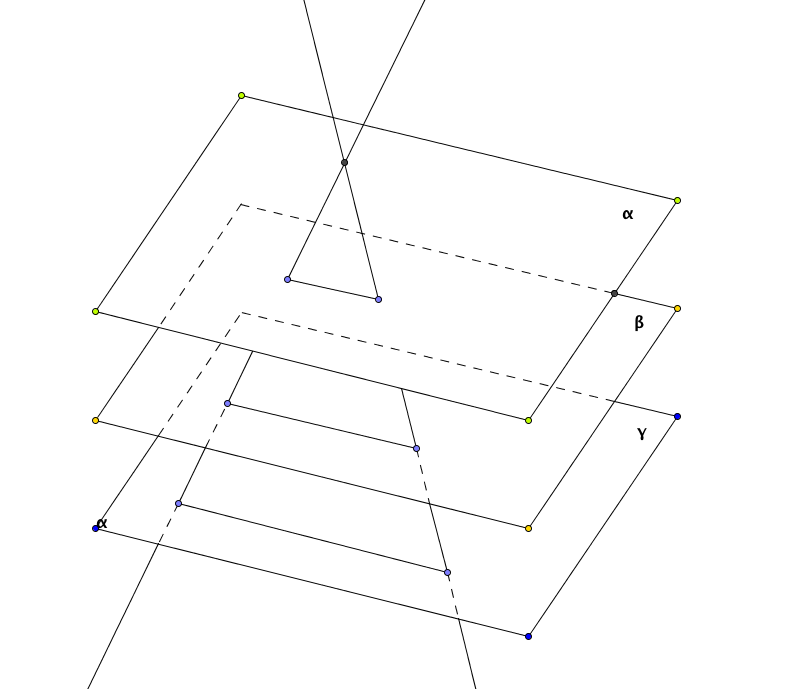
Teorema di Talete nello spazio

Un fascio di piani paralleli intersecati da due trasversali intercetta su di esse segmenti corrispondenti proporzionali.

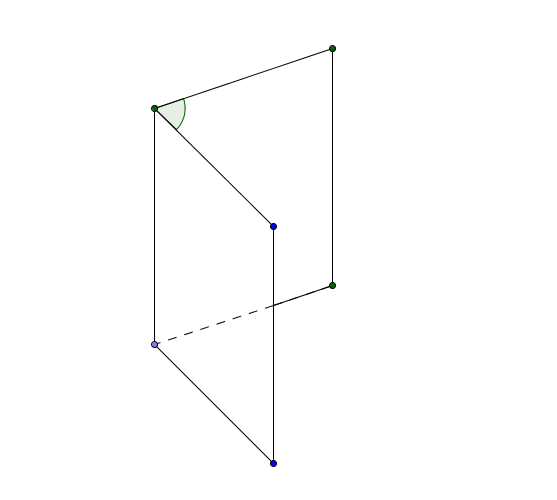
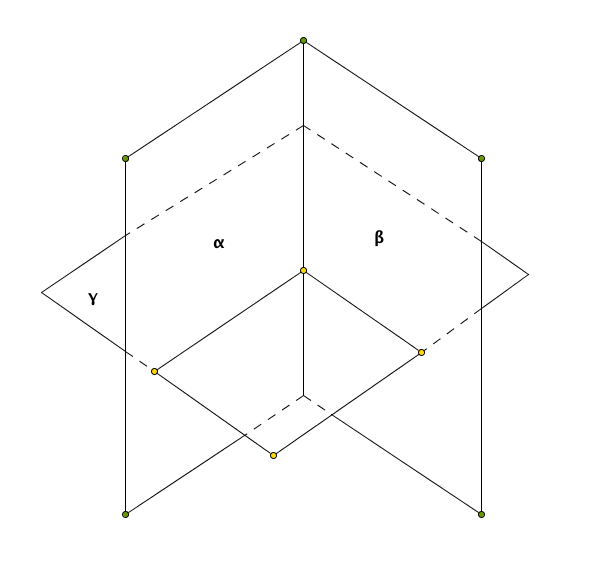
Diedro

Dati due semipiani aventi la stessa origine si chiama diedro ciascuna delle due parti di spazio tra essi comprese.

Sezione di un diedro

Si chiama sezione di un diedro l’angolo che si ottiene come intersezione fra il diedro e un qualunque piano non parallelo allo spigolo che interseca il suo spigolo.

• Sezioni parallele di uno stesso diedro sono congruenti.

• Due piani incidenti sono perpendicolari quando dividono lo spazio in quattro diedri retti.

• L’angolo di una retta r con un piano \alpha è l’angolo formato da r e dalla sua proiezione r' su a.

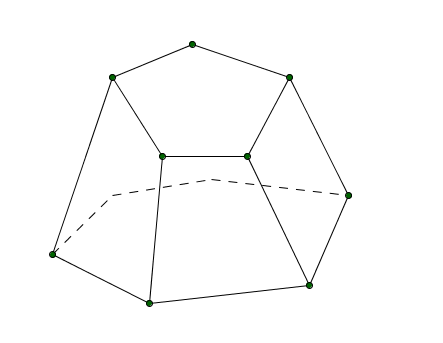
Poliedri

Un poliedro è una figura solida, limitata da un numero finito di poligoni, appartenenti a piani diversi, tali che il piano di ogni poligono non attraversi il solido.

I poligoni che compongono un poliedro sono dette facce e diagonali i segmenti che congiungono due vertici su facce diverse. Un poliedro ha almeno 4 facce.

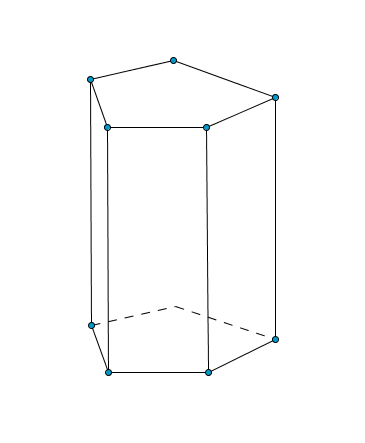
Prisma

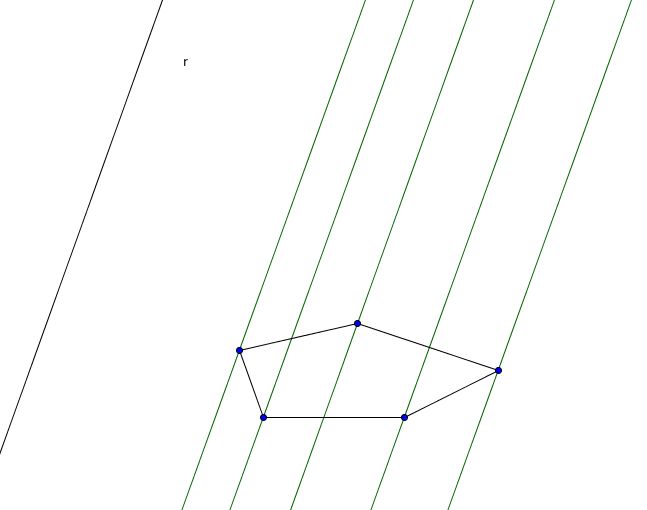
Prisma indefinito

Dato un poligono e una retta r, non appartenente al poligono, si dice prisma indefinito l'insieme di rette parallele a r passanti per il poligono.

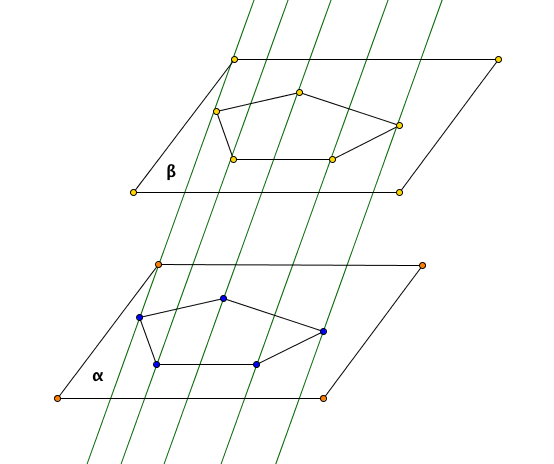
Prisma definito

Si dice prisma definito la parte di un prisma indefinito compresa tra due piani paralleli.

Prisma retto

Un prisma si dice retto un prisma che ha gli spigoli laterali perpendicolari ai piani delle basi.

Formule:

• superficie laterale: $$A_l = 2ph$$
• superficie totate: $$A_t = 2ph + 2A_b$$
• volume: $$V = A_b h$$

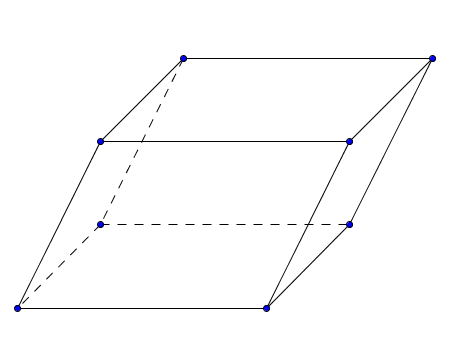
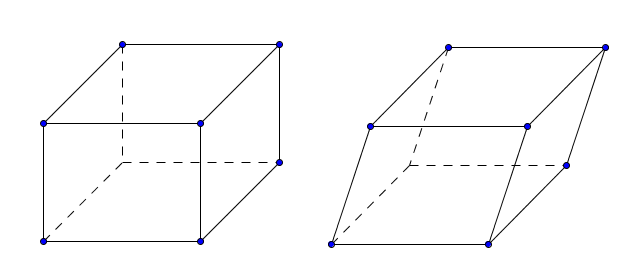
Parallelepipedo

Si dice parallelogramma un prisma le cui basi sono parallelogrammi.

Proprietà

• Un parallelepipedo ha le facce opposto congruenti e parallele.
• Le diagonali di un parallelepipedo si scambiano scambievolmente a metà.

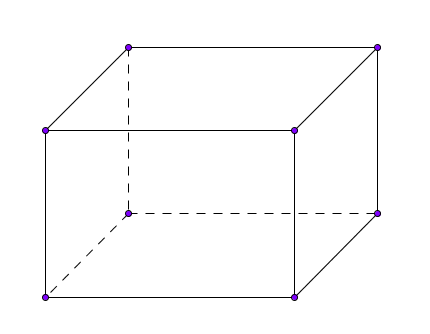
Parallelepipedo rettangolo

Si dice rettangolo un parallelepipedo che ha facce rettangolari.

Formule:

• superficie laterale: $$A_l = 2(a + b)c$$
• superficie totale: $$A_t = 2(ab + ac + bc)
• volume: $$V = abc$$

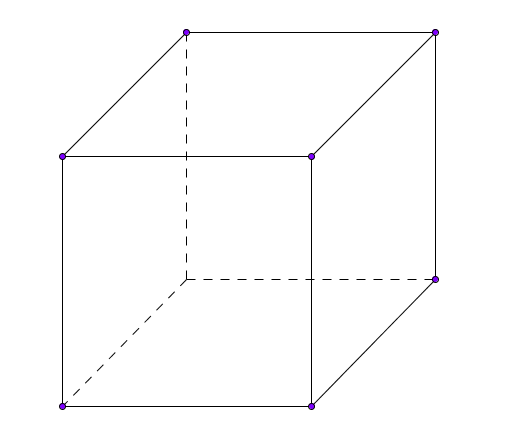
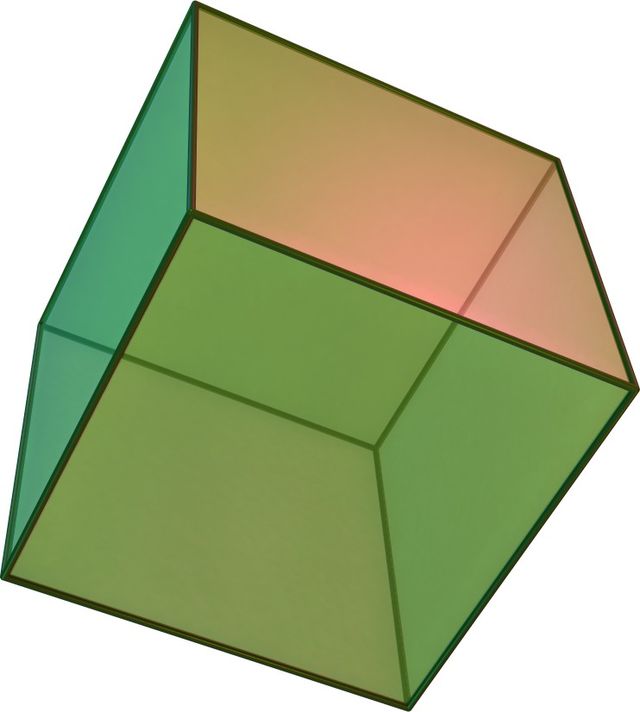
Cubo

Si dice cubo un parallelepipedo che ha facce quadrate tra loro congruenti.

Formule:

• superficie totale: $$A_t = 6s^2$$
• volume: $$V = s^3$$

Angoloide

Dato un poligono convesso e un punto V si dice angoloide l'insieme delle semirette uscenti da V e passanti per i punti del poligoni.

Le semirette passanti per i vertici del poligono sono dette spigoli, V vertice, gli angoli di vertice V e lati due spigoli consecutivi facce. Un angoloide con 3 facce si dice triedro.

Teoremi

• In un angoloide la somma degli angoli interni è minore dell'angolo giro.
• In un angoloide l'angolo di una faccia è minore della somma degli angoli delle altre facce.
• In un triedro l'angolo di una faccia è maggiore della differenza degli angoli delle altre facce.

Piramide

Si chiama piramide la parte di angoloide compresa tra il suo vertice ed un piano che lo interseca completamente.

Teoremi

In una piramide retta le altezze delle facce laterali passano per i punti di tangenza dei lati di base con la circonferenze inscritta e sono tra loro congruenti.

Piramide retta

Una piramide si dice retta se la sua base è circoscritta in una circonferenza di centro la proiezione del vertice sul piano della base.

Formule:

• superficie laterale: $$A_l = p a$$
• superficie totale: $$A_t = A_l + Ab + Ab'
• volume: $$V = \frac{1}{3}S h$$

Piramide regolare

Una piramide retta si dice regolare quando la sua base è un poligono regolare.

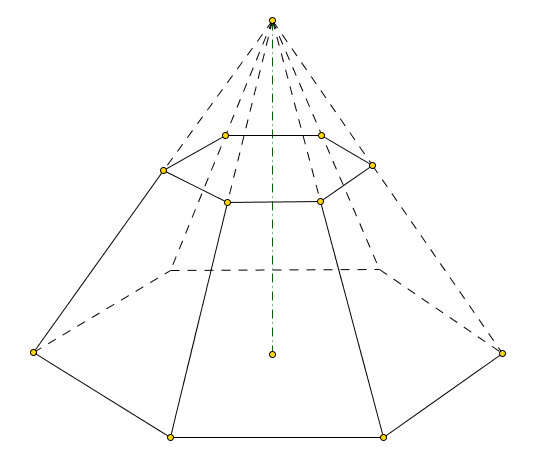
Tronco di piramide

Si chiama tronco di piramide la parte di piramide compresa tra due piani piani paralleli che la intersecano completamente.

Formule:

• superficie laterale: $$A_l=(p+p')a$$
• superficie totale: $$A_l=p a+Ab$$
• volume: $$V=\frac{1}{3}h(S+s+\sqrt{Ss})

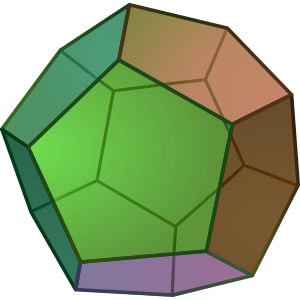
Poliedri regolari

Un poliedro si dice regolare quando le sue facce sono poligoni regolari congruenti e i suoi angoloidi e diedri sono congruenti.

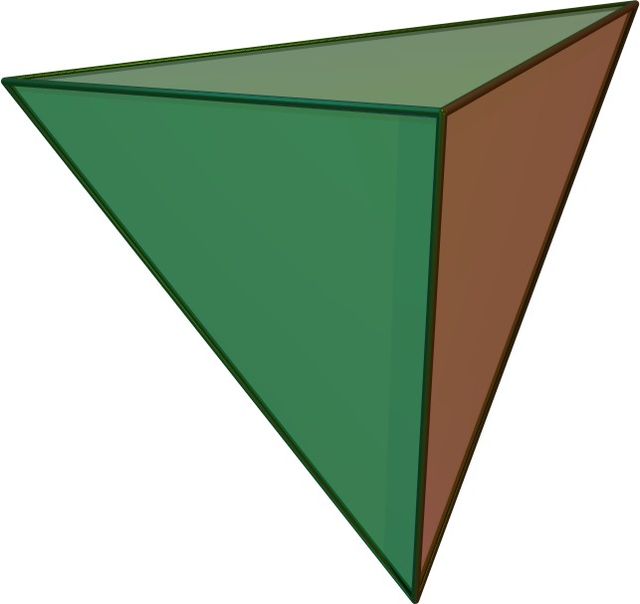
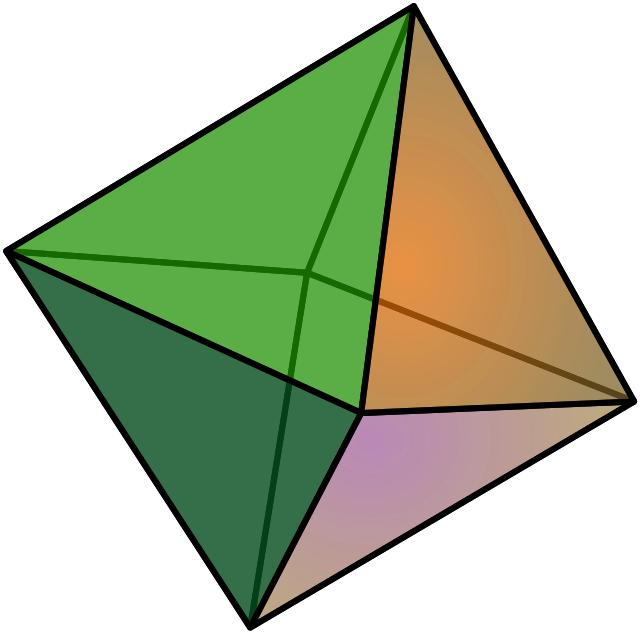
I poliedri regolari o solidi platonici sono 5: tetraedro, esaedro o cubo, ottaedro, dodecaedro e icosaedro.

poliedro	facce	vertici	spigoli	superficie	volume
tetraedro	4	4	6	s^2 \sqrt{3}	\frac{1}{12}s^3\sqrt{2}
esaedro	6	8	12	6s^2	s^3
ottaedro	8	6	12	2s^2 \sqrt{3}	\frac{1}{3}s^3\sqrt{2}
dodecaedro	12	20	30	15s^2 \sqrt{\frac{5+2\sqrt{5}}{5}}	s^3 \frac{15+7\sqrt{15}}{4}
icosaedro	20	12	30	s^2 5\sqrt{3}	s^3 \frac{5(3+\sqrt{5})}{12}

Solidi di rotazione

I solidi di rotazione sono figure solide ottenute dalla rotazione completa di un poligono attorno ad una retta.

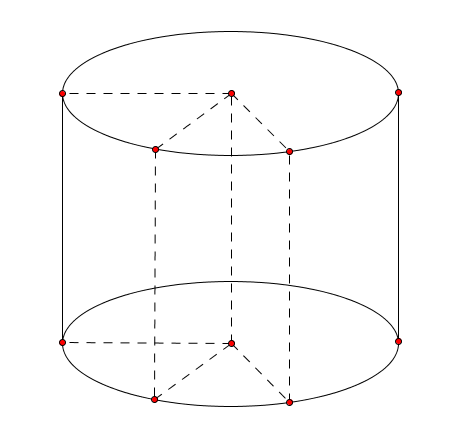
Cilindro

Si dice cilindro il solido ottenuto dalla rotazione completa di un rettangolo attorno ad un suo lato.

Formule:

• superficie laterale: $$A_l=2\pi rh$$
• superficie totale: $$A_t=2\pi r(h+r)
• volume: $$V=\pi r^2 h$$

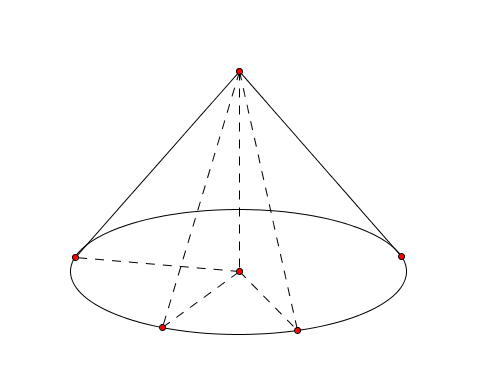
Cono

Si dice cono il solido ottenuto dalla rotazione completa di un triangolo rettangolo attorno ad un suo cateto.

Il cateto attorno a cui ruota il triangolo è l’altezza del cono, l’altro cateto è il raggio di base. L’ipotenusa è detta apotema del cono.

Un cono si dice equilatero se l’apotema è congruente al diametro della base.

Formule:

• superficie laterale: $$A_l=\pi ra$$
• superficie totale: $$A_t=\pi r(a+r)

In un cono, le misure delle aree del cerchio di base e del cerchio ottenuto da una sezione parallela al piano di base stanno tra loro come i quadrati delle misure delle loro distanze dal vertice.

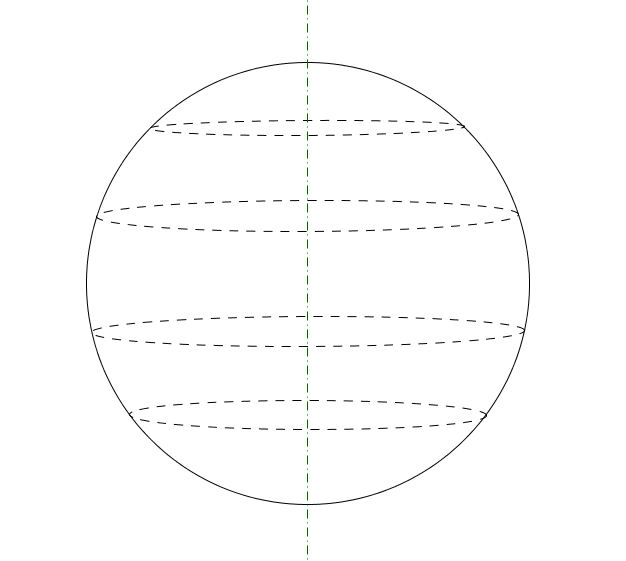
Sfera

Si dice sfera il solido ottenuto dalla rotazione di angolo piatto di una circonferenza attorno ad un suo diametro.

Formule:

• superficie totale: $$A_t=4\pi r^2$$
• volume: $$V=\frac{4}{3}\pi r^3$$

Equivalenza

Due solidi che hanno la stessa estensione sono equivalenti. L'equivalenza gode della proprietá riflessiva, simmetrica e transitiva.

Postulato n. 1

Due solidi congruenti sono sempre equivalenti ma non è detto il contrario.

Volume

Si dice volume di un solido la classe di equivalenza alla quale appartiene.

Somma di solidi

La somma di due solidi non intersecati è il solido ottenuto con l'unione di tutti i punti di tali solidi.

Postulato n. 2

Solidi ottenuti come somma di solidi congruenti sono tra loro equivalenti.

Postulato di De Zolt

Un solido non può essere equivalente ad una sua parte.

Un solido \mathscr{A} è maggiore di un solido \mathscr{B}, se \mathscr{B} è equivalente a una parte di \mathscr{A}. In tal caso si può dire che \mathscr{A} è prevalente a \mathscr{A}: \mathscr{A} > \mathscr{B}

Legge di esclusione

Dati due solidi \mathscr{A} e \mathscr{B} qualunque, o \mathscr{A} \doteq \mathscr{B} o \mathscr{A} > \mathscr{B} o \mathscr{A} < \mathscr{B}.

Equiscomponibilità

Due solidi di dicono equiscomponibili se è possibile dividerli in parti tra loro congruenti. Solidi equiscomponibili sono equivalenti.

Principio di Cavalieri

Se due solidi possono essere disposti in modo che vengano tagliati secondo sezioni equivalenti su ogni piano parallelo a un altro piano arbitrariamente fissato allora sono equivalenti.

Equivalenza dei solidi

Prismi

• Se due prismi hanno basi equivalenti e altezze congruenti allora sono equivalenti.
• Se un prisma e un cilindro hanno basi equivalenti e altezze congruenti allora sono equivalenti.

Piramidi

• Se due piramidi hanno basi equivalenti e altezze congruenti allora sono equivalenti.
• Una piramide è equivalente alla terza parte di un prisma che abbia la stessa base e la stessa altezza.
• Una piramide e un cono che hanno basi equivalenti e altezze congruenti sono equivalenti.

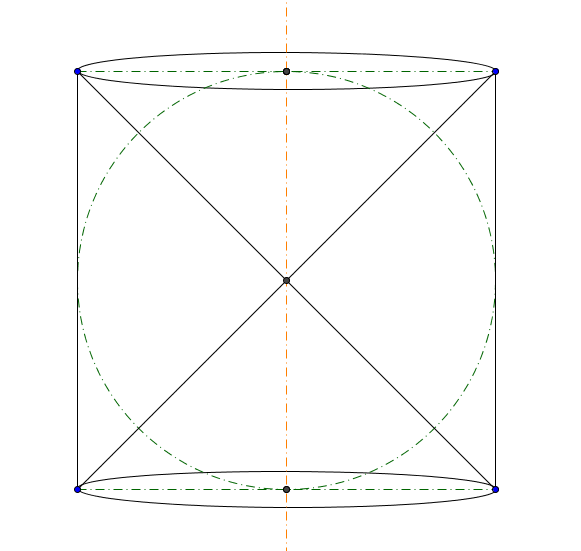
Anticlessidra

Si dice anticlessidra il solido ottenuto dalla differenza fra un cilindro equilatero circoscritto ad una sfera di centro O e due coni di vertice O di basi coincidenti con la base di tale cilindro.

Teorema
Una sfera \mathscr{S} è equivalente alla sua anticlessidra \mathscr{A}.

Dimostrazione
Sia \alpha il piano della base del cilindro e \alpha' un qualsiasi piano parallelo a \alpha. \alpha' interseca il cilindro ad un'altezza h da O, interseca il cono in A e la sfera in B.

Il triangolo \triangle{OHA} è simile al triangolo generatore dei coni dell'anticlessidra per il teorema di Talete. Pertanto è un rettangolo isoscele \Rightarrow \overline{AH} = h. La sezione di cilindro sul piano $\alpha$' individua una corona circolare di raggio r (raggio del cilindro) e raggio interno \overline{OA}, cioè h. La corona ha quindi area A=\pi r^2-\pi h^2 = \pi(r^2-h^2)

Il triangolo \triangle{OHB} è simile al triangolo generatore dei coni dell'anticlessidra per il teorema di Talete. Pertanto è un rettangolo. Per il teorema di Pitagora: \overline{HB}^2 = \overline{OB}^2 - \overline{OH}^2 = r^2 - h^2. La sezione di sfera sul piano \alpha' individua un cerchio di raggio HB. L'area del cerchio è quindi: A=\pi(r^2-h^2)

Il cerchio e la corona circolare sono equivalenti quindi per il principio di Cavalieri: \mathscr{S} \doteq \mathscr{A}

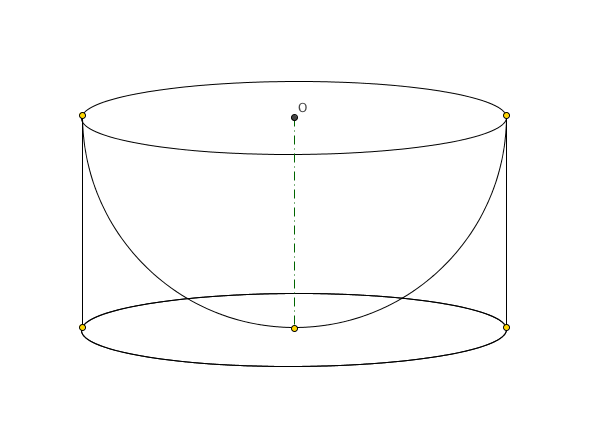
Scodella di Galileo

Si dice scodella di Galileo il solido ottenuto dalla differenza fra un cilindro di altezza uguale al raggio di base circoscritto ad una semisfera di centro O e la sfera stessa.

Teorema

La scodella di Galileo \mathscr{S} è equivalente al cono \mathscr{C} di vertice O e di base congruente alla base della scodella.

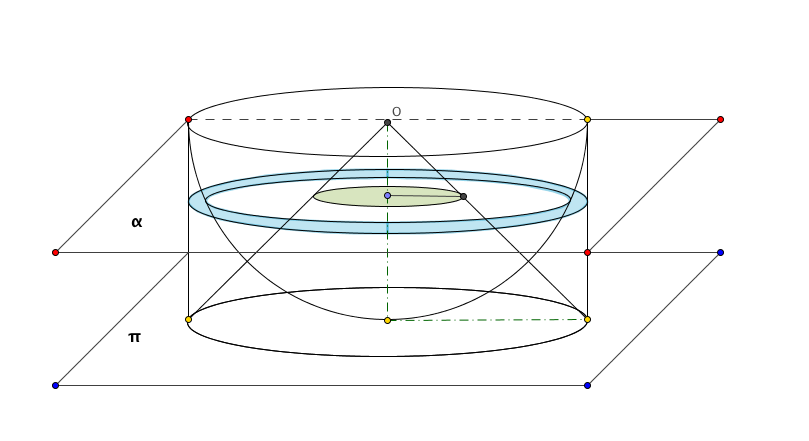
Dimostrazione
Sia \alpha un qualunque piano parallelo al piano della base \pi che intersechi \mathscr{S} e \mathscr{C} formando un cerchio S e una corona circolare S_1.

Siano A e B gli estremi del diametro della base della scodella su \pi.
Indicato con \delta il piano per A,B,O, \delta interseca \alpha in C e N. I punti in comune tra \alpha, \delta e la semisfera sono D e M e quelli tra \alpha, \delta e il cilindro sono E e Z. Infine sia H il piede della perpendicolare \mathscr{t} condotta da O ad \alpha e K l'intersezione tra \mathscr{t} e \pi.

OK \cong KB per definizione \Rightarrow \triangle KOB è rettangolo isoscele in K. \triangle OHN \sim \triangle KOB in quanto hanno \widehat{O} in comune e HN \parallel KB \Rightarrow \triangle OHN è isoscele \Rightarrow \overline{OH}=\overline{OK}.
Posto h = \overline{OH}, l'area del cerchio risulta A_S=\pi h^2

Considero \triangle OHM rettangolo: per il teorema di Pitagora: \overline{HM}=\sqrt{\overline{OM}^2-\overline{HM}^2} = \sqrt{r^2-h^2} (l'ipotenusa è il raggio della semisfera) L'area della corona circolare è pertanto: A_{S_1}=\pi\left(\overline{HZ}^2-\overline{HM}^2\right) = \pi [r^2 - (r^2 -h^2)] = \pi h^2

S \equiv S_1 per il principio di Cavalieri: \mathscr{S} \doteq \mathscr{C}